Second order differential equation solved with the Ti-84
Second-order differential equation solver (ODE2) (Trapezoidal method)
This TI-84 Basic program can solve second-order differential equations, which are useful for electrical (RLC) and mechanical (mass-spring, inertia-torsion) problems. It is advised, that if you have no experience with numerical programs to study the first-order differential equations examples first.
The general equation of a second order linear differential equation.
The function f(x) can be entered directly (mathematical definition) or by the program Funcgen.8xp.
Method: You must first create a signal using the Function Generator program, and then run the program for the second-order differential equation solver.
In the example we take voor A=1, B=0.5, C=1 and f(x) =1 for X< 5 and f(x)=0 for x>5
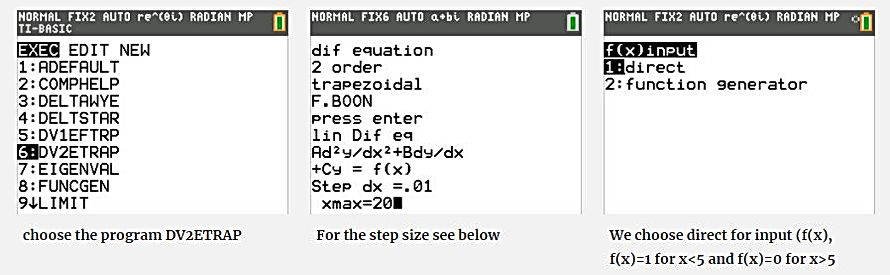
For numerical processes, the step size is an important parameter. Follow these rules:
Step size dx = < (√(A/C)) /20 = 0.05sec, or dx <(B/C)/10 = 0.05sec. Take the smallest step size of dx and therefore dx=0.05 sec. More info of the step size choice go to
Extra input programs have been added for the differential equation solvers, namely, Funcgen( make your own signal) and FUNCST1.8XP (square wave, pulse signal etc.). In the program, you can choose either direct input or a function generator as an input.
For information of the signal input generators, go to:
The third version DV2ETRV3 is now available with 999 calculated points stored.
Download the program DV2ETRV3.8xp:
